近日，成都大学高等研究院先进材料研究团队特聘研究员袁天宇与美国罗格斯大学的刘利平教授合作，针对细观力学夹杂构型与内场的关联性问题，在经典椭球构型的基础上提出了一种全新的夹杂构型—多项式类区域。该研究以” Polynomial inclusions: Definitions, applications, and open problems”为题在线发表于国际固体力学旗舰期刊《Journal of the Mechanics and Physics of Solids》(https://authors.elsevier.com/c/1hocw57Zk5KLA)。

        从场论的角度来看，大多数物理定律都可以被描述为微分方程，譬如牛顿的万有引力理论、麦克斯韦的电磁场理论、爱因斯坦的广义相对论等等。这些经典理论的预测依赖于相应微分方程边值问题的解，方程的求解难度由微分方程的结构及边界的几何形状决定。椭球构型的边界常常能为求解提供极大的便利性，由此衍生出许多意义深远的结果，例如，均匀椭球区域的牛顿位势在其内部为空间坐标的二次函数；均匀极\磁化的椭球区域内部会产生均匀的电\磁场；爱因斯坦引力场方程在球域外存在封闭形式的施瓦氏解。近代细观力学领域重要的奠基性工作也与椭球构型密不可分，英国学者Eshelby于1957年求解了各向同性无限大介质中经受均匀本征应变场的椭球夹杂内部的弹性场，发现椭球内部弹性应变场也是均匀的，由此衍生出一系列创新概念和方法，开启了非均质力学理论高速发展的新时代。

        然而，在自然界和工程实际中，严格椭球形的研究对象往往很稀少，大多数实际力学、物理问题都需要考虑非椭球的研究对象。在夹杂理论的研究中，就常常需要处理非椭球夹杂问题，例如，在近年来用于量子信息通信的半导体量子点材料中，主导其物理性能的量子点夹杂就可能为多面体、圆柱体、截棱锥、甚至呈树枝状，而这些复杂的夹杂构型也为材料内部应力场的计算以及相应力学、物理性能的精确预测带来极大的困难。

        由于复杂夹杂构型内部非均匀的内场可以近似为多项式形式来考虑，问题的精度由多项式的截断程度决定，本文基于夹杂问题解的形式首次逆向构建了一类特殊的夹杂构型—多项式类区域，由其产生的力学、物理场能解析、简洁地表示为空间坐标的多项式形式，且椭球为该类夹杂构型的特例。利用复变函数、位势理论、变分不等式等方法，可构建从二维到任意维的多项式类区域，二维及三维的示例如图1所示。

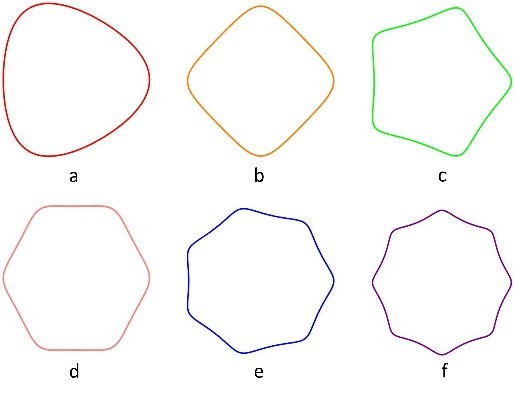
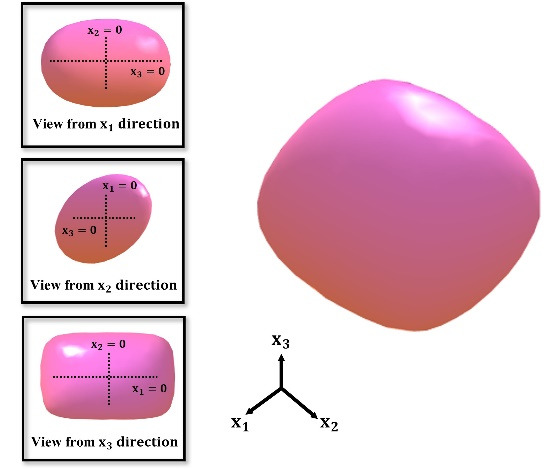
(a) 二维多项式类区域示例                                                    （b）三维多项式类区域示例

图1. 多项式类区域示例

        本文深入探索了多项式类区域的数学、力学性质，系统研究了多项式类区域Eshelby问题、极\磁化问题解的具体形式。这分别具有数学和力学两个层面的意义，从数学层面上讲，本文对多项式类区域存在性、几何性质及表示方法的研究可帮助促进代数拓扑方法的发展，同时也为建立微分方程边值问题的解与其边界几何形状之间的联系提供了新的研究思路；从力学层面上讲，多项式类区域是对经典椭球夹杂构型的推广，其良好的性质，即力学、物理场可简单表达为空间坐标的多项式形式，为复合材料性能设计和预测提供了新的维度，图2及图3分别展示了通过多项式类区域设计的两类复合材料结构，其中图2中结构产生的多极磁场可被用于约束环磁机、仿星器等核聚变装置中的高温离子束，从而提升装置的整体安全性。

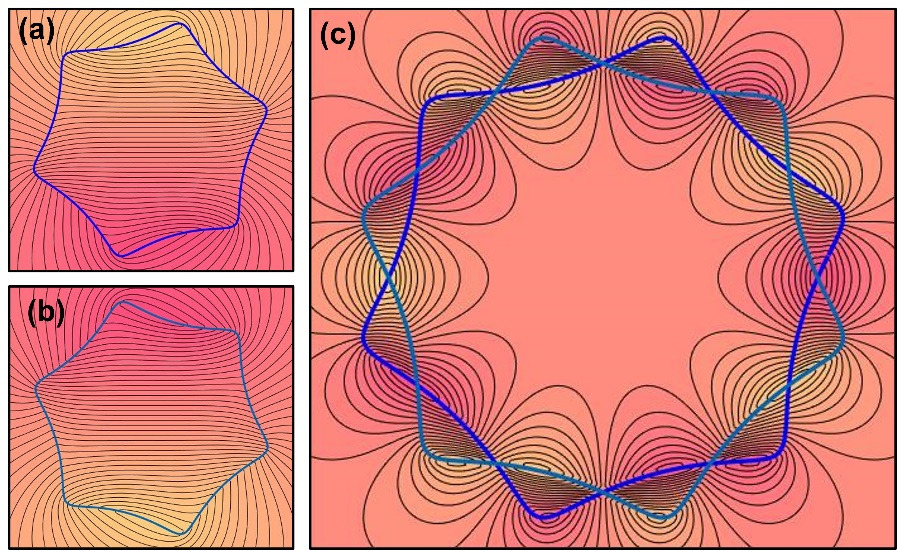
图2. 基于多项式类区域设计二维结构实现十极的多项式磁场

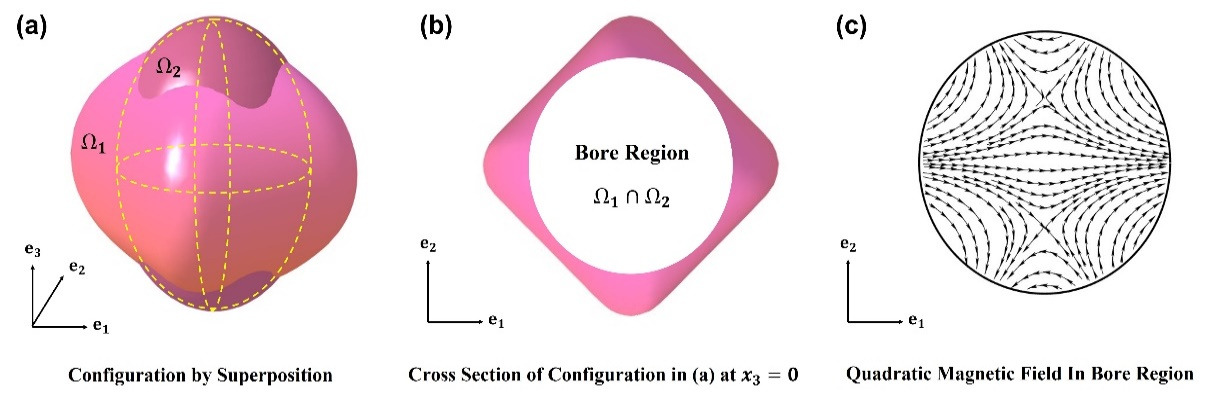
图3. 基于多项式类区域设计三维结构实现平面的多项式磁场